K問題：Black and White Boxes - tshitaの備忘録Ⅱ

1. 概要

これは Competitive Programming （その2） Advent Calendar 2016 - Adventar の22日目の記事です．

今年のACM-ICPC 2016アジア地区つくば大会のK問題で組合せゲーム理論に関する問題が出題されました．この問題を通して組合せゲーム理論の紹介をします ~~(考察が中途半端になってしまいました)~~．
2017年1月5日に追記・修正しました．

解説等は公開されています．

問題： Problem K : Black and White Boxes
判定データ： http://icpc.iisf.or.jp/past-icpc/regional2016/judge-data/K/
講評： http://icpc.iisf.or.jp/past-icpc/comments/2016.pdf#page=5
講評スライド： http://icpc.iisf.or.jp/past-icpc/comments/2016-slides.pdf#page=56
オンラインジャッジ : Black and White Boxes | Aizu Online Judge

natsugiriさんの分かりやすい解説があります．
ACM-ICPC 2016 Asia Tsukuba Regional, K 解法 - でも今日はSRMあるから

組合せゲーム理論の参考書として次の本を参考にしました．

組合せゲーム理論入門 ?勝利の方程式?

作者: M.H.Albert,R.J.Nowakowski,D.Wolfe,川辺治之
出版社/メーカー: 共立出版
発売日: 2011/09/21
メディア: 単行本
クリック: 5回
この商品を含むブログ (1件) を見る

1.1 [問題] Black and White Boxes (BWB)

アリスとボブの2人で行うゲーム．

直立に積み重なった箱の山がいくつかある．各々の箱は同じ大きさで白色か黒色に塗られている．
アリスとボブが交互に手を打つ．先手のプレイヤーは公平に無作為に選ばれる．
アリスの手番：1つの山から黒色の箱を1つ選び，その箱とその上にあるすべての箱を取り除く．
ボブの手番：1つの山から白色の箱を1つ選び，その箱とその上にあるすべての箱を取り除く．

自分の手番で手を打つことができなければそのプレイヤーの負け．

どのプレイヤーが先手でも先手勝ち，または，どのプレイヤーが後手でも後手勝ちとなる初期局面のことを公平な初期局面という．n個の山が与えられる．その中からいくつかの山を選び初期局面とする．公平な初期局面の中ですべての山の箱の数の和が最大となるものを求めそのときの箱の数を答えよ．

制約：n <= 40. 各々の山に含まれる箱の数 <= 40

1.2 [山の表記方法]

今後，この問題を短くBWBゲームと呼ぶことにします．
説明の為に一つの山を文字列として表します．Bを黒色の箱，Wを白色の箱として，文字列の左から右に向かって山の下から上に対応しているとします．便宜上，箱がない山を _ (アンダーバー) で表します．また，複数の山からなる局面を . (ピリオド)で区切ることにします．

例：1つの山）
　WBBW は下から白色，黒色，黒色，白色の四つの箱からなる一つの山

例：複数の山)

WBBW.WB は二つの山からなる局面で1番目の山はWBBW，2番目の山はWB
WW._.W.B は三つの山からなる局面で1番目の山はWW，2番めの山は空，3番目の山はW，4番目の山はB

2. 組合せゲーム理論とは？

組合せゲーム理論(combinatorial game theory)とは組合せゲームを解析する理論です．組合せゲームは大雑把にいうと二人有限確定完全情報ゲームです．

二人：二人のプレイヤーが交互に手を打つゲーム
有限：有限の手数で終了する
確定：偶然に左右される要素がない
完全情報：対局者はゲームの局面についての情報をすべて知っている

組合せとついているのは経済学などで現れるゲーム理論と区別するためです．BWBゲームは組合せゲームになります．

2.1 [対局者]

慣習として組合せゲームの二人の対局者を左と右と呼びます．BWBゲームではアリスとボブをそれぞれ左と右と呼ぶことにします．．どちらの対局者が先手番となるかが重要なときには左，右ではなくアリスとボブと呼ぶそうです．ここでは慣習にしたがい左と右と呼ぶことにします．
一般的には最後の手を打った対局者が勝ちとなりそのようなゲームを正規形 (normal play) と呼びます．BWBゲームは打つ手が存在しない対局者の負けなので正規形です．逆に，最後の手を打った対局者が負けとなるゲームを逆形　(misere play) と呼びます．逆形のゲームは正規形のゲームと比べると解析が難しくなります．

2.2 [選択肢(option)]

与えられたゲームの局面に対して左が手を打って得られる局面をその局面の左選択肢 (left option) と呼びます．同様に，右が打って得られる局面を右選択肢 (right option) と呼びます．また，それぞれを区別しない場合はその局面の選択肢と呼ぶことにします．
ゲームの局面を頂点として左選択肢をその頂点の左下，右選択肢をその頂点の右下にくるように配置して得られる根付き木をゲーム木 (game tree) と呼びます．一般的なゲーム木とは異なるので注意してください．一般的なゲーム木では左選択肢と右選択肢が異なる高さで交互に現れますが，ここで扱うゲーム木は同じ高さに左選択肢と右選択肢が現れる可能性があります．

例：WBBWのゲーム木 )
WBBWというゲームに対して，左(アリス)は下から2番目の箱を選ぶか，下から3番目の箱を選ぶかの2つがあります．各々の手に対する左選択肢はWBとWでWBBWの左下に配置します．
f:id:tatanaideyo:20161222091102p:plain

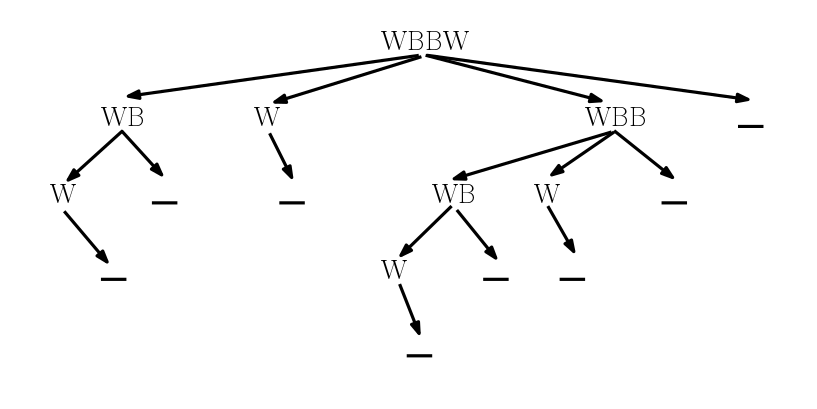
3. 組合せゲームとは？

ゲームの局面をゲームと呼ぶことにします．先ほどのゲーム木の各々の頂点がそれぞれゲームになります．

3.1 [組合せゲーム]

[定義：ゲーム (の局面)]
ゲーム (の局面) $G$ を $G = \{\mathscr{g}^L \mid \mathscr{g}^R\}$ とする．
ただし， $\mathscr{g}^L$ と $\mathscr{g}^R$ はそれぞれ左選択肢の集合と右選択肢の集合とする．

また， $G^L, G^R$ でそれぞれ $\mathscr{g}^L, \mathscr{g}^R$ の要素の代表を表すことにします．

例：ゲーム (の局面) WBBW )
　 $WBBW = \{WB, W \mid WBB, \_\}$
ここで，左選択肢の集合と右選択肢の集合はそれぞれ， $\mathscr{g}^L = \{WB, W\}$ と $\mathscr{g}^R = \{WBB, \_\}$ になります．通常，左選択肢の集合と右選択肢の集合は集合なので「{} 」(ブレース)で選択肢を囲みますが簡略化のために省略して表記します．

余談ですが，左選択肢と右選択肢が等しいゲームを不偏 (impartial)ゲームと言います．また，不偏ゲームでないゲームのことを非不偏 (partizan) ゲームと言います．今回のBWBゲームは非不偏ゲームですが，左も右も色に関わらずどの箱も取り除くことができるとルールを変えたゲームは不偏ゲームでニムと呼ばれる有名なゲームになります．
すべての不偏ゲームはニムと等価 (グランディー数が存在)であるという美しい結果が知られています．一般に，非不偏ゲームは不偏ゲームよりも解析が難しいです．
Advent Calendarの12日目のzukky162さんの記事で「グランディ数」について書かれているので興味のある方はどうぞ．
zukky162.hatenablog.com

3.2 [帰結類 (outcome class)]

組合せゲームでは，与えられたゲーム (の局面)に対して各々の対局者が最善の手を打った場合にどの対局者が勝つのかに興味があります．最善の手とは勝つことができるならそのような勝つことのできる手を打ち，勝つことができないならただ手を打つことです．
ゲーム (の局面) $G$ が与えられ $G$ からゲームを行ったときに起きうる結果は次の4通りです．この起きうる結果のことを帰結類 (outcome class) と呼びます．行いたいことは初期局面 (ゲーム) が与えられたときにそのゲームの帰結類を求めることです．

表1. 帰結類
帰結類	名称	定義
$\mathscr{N}$	ファジー	先手番(Next : 次)の対局者が必ず勝つ
$\mathscr{P}$	零	後手番(Previous : 直前)の対局者が必ず勝つ
$\mathscr{L}$	正	どちらが先手番でも左(Left)が勝つ
$\mathscr{R}$	負	どちらが先手番でも右(Right)が必ず勝つ

すべてのゲーム (の局面) は $\mathscr{N}, \mathscr{P}, \mathscr{L}, \mathscr{R}$ の帰結類のちょうど1つに属します．ここで， $\mathscr{N}, \mathscr{P}$ に属するゲーム (の局面) をそれぞれ $\mathscr{N}$ 局面， $\mathscr{P}$ 局面と呼ぶことにします．
ゲーム $G$ の帰結類はゲーム木を見ることで分かります．ゲーム木の葉はその局面で選択肢が無いので後手勝ちとなります．すなわち葉は $\mathscr{P}$ 局面です．葉から順番に次の表にしたがって帰結類を決定していきます．

表2. 選択肢と帰結類の関係
	$\exists G^R \in \mathscr{R} \cup \mathscr{P}$	$\forall G^R \in \mathscr{L} \cup \mathscr{N}$
$\exists G^L \in \mathscr{L} \cup \mathscr{P}$	$\mathscr{N}$	$\mathscr{L}$
$\forall G^L \in \mathscr{R} \cup \mathscr{N}$	$\mathscr{R}$	$\mathscr{P}$

この表の見方は，例えば $G$ が $\mathscr{N}$ 局面(2行2列)となるのは，「 $\exists G^L \in \mathscr{L} \cup \mathscr{P}$ 」と「 $\exists G^R \in \mathscr{R} \cup \mathscr{P}$ 」が成り立つ場合です．すなわち，先手勝ちとなるのは，左が先手番のときに左勝ち (左の選択肢に左勝ちまたは後手勝ちとなる手が存在する)，右が先手番のときに右勝ち(右の選択肢に右勝ちまたは先手勝ちとなる手が存在する)となることです．
また，左選択肢が存在しない場合「 $\forall G^L \in \mathscr{R} \cup \mathscr{N}$ 」は成り立ちます．同様に，右選択肢が存在しない場合「 $\forall G^R \in \mathscr{L} \cup \mathscr{N}$ 」は成り立ちます．このことからも葉の帰結類が $\mathscr{P}$ となることが分かります．

例：ゲーム WBBWの帰結類 )
WBBWに対して表2を適用した結果が下のゲーム木(頂点に帰結類を表示)になります．WBBWの帰結類は $\mathscr{R}$ となるので，どちらが先手番でも右が必ず勝ちます．
f:id:tatanaideyo:20161222093423p:plain

4. ゲームの代数

ここまでで，初期局面の帰結類はゲーム木が分かれば決定することができるということを見てきました．しかし，一般的にゲーム木を知るというのは時間がかかるので他の方法で簡単に帰結類が決定できれば嬉しいです．
ここでは，帰結類を決定するのに役立つゲームの道具について見ていきます．

4.1 [ゲームの直和]

お互いに独立なゲーム $G, H$ の直和 $G + H$ を定義します．お互いに独立なゲームとは片方のゲームに手を打っても片方のゲームに影響を与えない2つのゲームです．
例えば，2つの山 WBBW.BW からなるBWBゲームを考えます．対局者は1番目の山WBBWに手を打つとします．このとき，2番目の山はBWのままで影響がありません．同様に，2番目の山に手を打っても1番目の山には影響がありません．したがって，ゲームWBBW とBWはお互いに独立なゲームとなります．BWBゲームでは各々の山をゲームとしたとき，山同士はお互いに独立となっています．
ゲームの直和とは直和成分 $G, H$ を並べて1つのゲーム $G + H$ としたものです．対局者はどの直和成分にも手を打つことができます．これをきちんと定義したものが次になります．

[定義：ゲームの直和]
ゲーム $G$ と $H$ の直和 $G + H$ を
　 $\{\mathscr{g}^L + H, G + \mathscr{h}^L \mid \mathscr{g}^R + H, G + \mathscr{h}^R \}$
とする．
ただし，選択肢の集合 $\mathscr{g}$ とゲーム $G$ の直和 $\mathscr{g} + G$ を，
　 $\bigcup_{X \in \mathscr{g}} X + G$
とする．

上の定義からゲームの直和 $G + H$ もゲームです．また，選択肢の集合の和集合を簡略化のために「,」(カンマ)で表記します．
各々の直和成分の帰結類が分かっているときにそれらの直和が簡単に分かると嬉しいのですがBWBゲームでは簡単に分かります．すなわち，各々の山の帰結類が分かっているときに，それらの山からなるゲームの帰結類も簡単に分かります．このことについてはゲームの値で見ていきます．

例：ゲームWBBW, BWの直和)
互いに独立なゲームを
　 $G =$ WBBW $= \{WB, W \mid WBB, \_\}$
　 $H =$ BW $= \{\_ \mid B\}$
とする．
各々の左選択肢の集合と右選択肢の集合は次の通りになる．
　 $\mathscr{g}^L = \{WB, W\}, \mathscr{g}^R = \{WBB, \_\}$
　 $\mathscr{h}^L = \{\_\}, \mathscr{h}^R = \{B\}$
このとき，
　 $\mathscr{g}^L + H = \{WB + BW, W + BW\}$
　 $G + \mathscr{h}^L = \{WBBW + \_\}$

　 $\mathscr{g}^R + H = \{WBB + BW, \_ + BW\}$
　 $G + \mathscr{h}^R + H = \{WBBW + B\}$
となる．
したがって $G$ と $H$ の直和は
　 $G + H = \{WB + BW, W + BW, WBBW + \_ \mid WBB + BW, \_ + BW, WBBW + B\}$
となる．

4.2 [ゲームの(符号)の反転]

ゲームの符号の反転は再帰的にゲームの対局者の役割を入れ替えます．

[定義：ゲームの(符号)の反転]
ゲーム $G$ の符号の反転 $-G$ を
　 $\left\{-\mathscr{g}^R \mid -\mathscr{g}^L\right\}$
とする．
ただし，
　 $-\mathscr{g}^R = \bigcup_{G^R \in \mathscr{g}^R} \left\{-G^R\right\}$
　 $-\mathscr{g}^L = \bigcup_{G^L \in \mathscr{g}^L} \left\{-G^L\right\}$
とする．

例：ゲームWBBWの反転 )
始めに， $\_ = \{ \mid \}$ から $-\_ = \{ \mid \} = \_$ である．
WBBWのゲーム木と上の定義によって再帰的に反転させた-WBBWのゲーム木は次の通りである．左がWBBWのゲーム木，右上が反転させた-WBBWのゲーム木，右下がゲーム木の形とBWBゲームのルールから考察したときのゲーム．

f:id:tatanaideyo:20161222091102p:plain:w300

-WBBWのゲーム木を見てBWBゲームのルールを思い返すと， $\{\_ \mid \}$ となるゲームは B になります． -WBBWのゲーム木で-WをBに交換します．次に， $\{\_ \mid B\}$ となるゲームは BW となるので，-WB を BW に交換します．次に， $\{\_ \mid BW, B\}$ となるゲームは BWW なので -WBB を BWW に交換します．最後に， $\{BWW, \_ \mid B, BW\}$ となるゲームは BWWB なので -WBBW をBWWB に交換します．
すなわち，-WBBW は BWWB となります．BWBゲームではゲームの反転は黒箱を白箱に，白箱を黒箱にを入れ替えたゲームになります．

4.3 [ゲームの等価性]

2つのゲームが等しいことを次のように定義します．

[定義：ゲームの等価性]
ゲーム $G$ と $H$ の等価性 $G = H$ を
　すべてのゲーム $X$ に対して， $G + X$ と $H + X$ が同じ帰結類に属する
こととする．

この定義からゲームが等価であることを判定するのは大変そうです．そこで，判定しやすい同値な定義を紹介します．その前に特別なゲームに名前を付けます．

[定義：零ゲーム]
$0 = \{ \mid \}$ とする．

上の定義は左選択肢と右選択肢のないゲームの名前を0とするということを表しています．0は選択肢が無いので $\mathscr{P}$ 局面です．帰結類のところで帰結類 $\mathscr{P}$ の名称を零としましたがこれは次の定理によるものです．

[定理： $\mathscr{P}$ 局面と零ゲームの等価性]
ゲーム $G$ が $\mathscr{P}$ 局面 $\Leftrightarrow$ $G = 0$

任意のゲーム $G, H$ に対して次の表のことが成り立ちます．

表3. ゲームの比較と帰結類
$G > 0$ $\Leftrightarrow$ $G$ は左の勝ち	$G > H$ $\Leftrightarrow$ $G - H$ は左の勝ち
$G = 0$ $\Leftrightarrow$ $G$ は後手番の勝ち	$G = H$ $\Leftrightarrow$ $G - H$ は後手番の勝ち
$G < 0$ $\Leftrightarrow$ $G$ は右の勝ち	$G < H$ $\Leftrightarrow$ $G - H$ は右の勝ち
$G \parallel 0$ $\Leftrightarrow$ $G$ は先手番の勝ち	$G \parallel H$ $\Leftrightarrow$ $G - H$ は先手番の勝ち

ここで， $G \ge 0$ は $G > 0$ または $G = 0$ です．すなわち，ゲーム $G$ において左が後手番で勝つことを表しています．同様に， $G \le 0$ は $G < 0$ または $G = 0$ でゲーム $G$ において右が後手番で勝つことを表しています．また， $G - H$ が先手番の勝ちならば $G \ge H$ でも $G \le H$ でもないので， $G$ と $H$ は比較不能であるとして $G \parallel H$ と表します．
$\ge$ と $\le$ はゲームの全体上で半順序となります．また，二項演算を $+$ ， $G$ の逆元を $-G$ ，単位元を0 (零ゲーム) とするとゲームの全体上で可換群となります．
ゲームの等価性の定義に従って $G = H$ を示すよりも， $G - H$ というゲームにおいて後手勝ちとなることを示す方が簡単です．

例：ゲームBの反転 )
表3を使うとゲームBの反転ゲームが分かります．
$G =$ B $= \{\_ \mid \}$ , $H =$ W $= \{ \mid \_\}$ とする．
ゲームB.W ( $G + H$ ) は後手勝ちのゲームなので， $G + H = 0$ ．
すなわち， $H = -G$ となるので，ゲームBの反転ゲームはWとなる．

4.3 [ゲームの標準形 (canonical form)]

4.2では帰結類の観点からゲーム木の形が異なっていても等しいゲームというものを定義しました．もちろんゲーム木が同じであれば帰結類も等しくなります．ここでは，帰結類を保ちながらゲーム木を小さくする方法を紹介します．初めにその方法を2つ紹介します．

[定義：劣位な選択肢]
ゲーム $G = \{L_1, L_2, \ldots \mid R_1, R_2, \ldots \}$

左選択肢において， $L_i \ge L_j$ のとき， $L_j$ を劣位な選択肢と呼ぶ．
右選択肢において， $R_i \le R_j$ のとき， $R_j$ を劣位な選択肢と呼ぶ．

劣位な選択肢の除去はその手よりも良い手があるならば良い手を選択するので選ばないという直感的な操作になります．

例：劣位な選択肢の除去 )
ゲームWBBW $= \{WB, W \mid WBB, \_\}$ に対して劣位な選択肢の除去を行います．

WB $\ge$ W ： $WB - W = WB + B$ において左が後手勝ちになる
WBB $\le$ _ ： $WBB - 0 = WBB$ において右が後手勝ちになる

したがって，左選択肢の W と右選択肢の _ は劣位な選択肢となります．ゲームWBBW において劣位な選択肢の除去を行ったゲームは
　 $\{WB \mid WBB\}$
となります．

次に打消し可能な選択肢を紹介します．打消し可能な選択肢は重要なのですがBWBゲームでは使わないので定義だけ行います．

[定義：打消し可能な選択肢]
ゲーム $G = \{L_1, L_2, \ldots \mid R_1, R_2, \ldots \}$

左選択肢 $L_i$ のある右選択肢 $L_i^R$ に対して， $G \ge L_i^R$ が成り立つとき， $L_i$ を打消し可能な選択肢と呼ぶ．
右選択肢 $R_i$ のある左選択肢 $R_i^L$ に対して， $G \le R_i^L$ が成り立つとき， $R_i$ を打消し可能な選択肢と呼ぶ．

打消し可能な選択肢 $L_1$ のある右選択肢が $L_1^R = \{L'_1, L'_2, \ldots, \mid \ldots \}$ のとき，
　 $\{L'_1, L'_2, \ldots, L_2, \ldots \mid R_1, R_2, \ldots\}$
を $L_1$ の短絡と呼ぶ．
打消し可能な選択肢 $R_1$ のある左選択肢が $R_1^L = \{\ldots, \mid R'_1, R'_2, \ldots \}$ のとき，
　 $\{L_1, L_2, \ldots \mid R'_1, R'_2, \ldots, R_2, \ldots \}$
を $R_1$ の短絡と呼ぶ．

上の2つの操作を行ってゲーム木を小さくします．

[定義：ゲームの標準形 (canonical form)]
ゲーム $G$ の全局面に対して次の2つの操作

劣位な選択肢の除去
打消し可能な選択肢の短絡

を行うことによって得られるゲームを $G$ の標準形(canonical form)と呼ぶ．

ゲームの標準形とゲームの等価性には次の関係があります．

[定理：ゲームの標準形と等価性の関係]
ゲーム $G, H$

$G, H$ は標準形かつ $G = H$ 　 $\Leftrightarrow$ 　 $G$ と $H$ は同型

$G$ と $H$ のゲーム木が根付き木として同じ形をしているとき $G$ と $H$ は同型であるとします．
すべてのゲーム $G$ の標準形は操作の順序に関わらず一意に定まります．また，標準形はゲームの等価性を保つものの中で最小のゲーム木となります．ゲームの標準形を考えることによってゲームの解析の見通しが良くなります．

5. ゲームの値

組合せゲーム理論ではいくつかの重要なゲームの標準形に名前を付けています．先ほど $\{ \mid \}$ という形のゲームに0という名前をつけました．これらの重要なゲームに対する名前をゲームの値と呼ぶことにします．
ほとんどのゲームの値に対して，その帰結類，ゲームの値同士の直和やその帰結類を求めることは簡単ではありません．しかし，BWBゲームで現れる全てのゲームには数という値がついておりこれらの計算が簡単にできます．

[定義：整数]
正整数 $n$ に対して，
　 $n = \{n - 1 \mid \}$
　 $-n = \{ \mid 1 - n\}$
とする．
ただし， $0 = \{ \mid \}$ ．

これらは， $\{n - 1 \mid \}$ という形をしたゲームに値 $n$ を割り当てるということに注意してください．
例えば， $1 = \{0 \mid \} = \{\{ \mid \} \mid \}$ , $-2 = \{ \mid -1\} = \{ \mid \{ \mid 0\}\} = \{ \mid \{ \mid \{ \mid \}\}\}$ を表しています．

f:id:tatanaideyo:20170105001104p:plain:w400

例：ゲームB, WW)
ゲームの定義に従ってゲームBとWWを表します．ここで， $\_ = \{ \mid \} = 0$ だったことに注意してください．
　 $B = \{\_ \mid \} = \{0 \mid \} = 1$
　 $WW = \{ \mid W, \_\} = \{ \mid W\} = \{ \mid \{ \mid \_\}\} = \{ \mid \{ \mid 0\}\} = -2$

WWの左から2つ目の等号では $W < \_$ から劣位な選択肢の除去を行っています．
ここで，Bのゲーム木の形と1のゲーム木は等しいので $B = 1$ となります．同様に，WWのゲーム木と-2のゲーム木は等しいので $WW = -2$ となります．帰納的に， $n$ 個の黒箱からなる山のゲームの値は $n$ ， $n$ 個の白箱からなるゲームの値は $-n$ となります．

整数という名前から次のことが成り立ちます．

[定理：ゲームの値が整数のゲーム]
ゲーム $A, B, C$ とそれぞれの整数のゲームの値を $a, b, c \in \mathbb{Z}_{+}$

$A + B = C$ $\Leftrightarrow$ $a + b = c$
$A \ge B$ $\Leftrightarrow$ $a \ge b$
$A \le B$ $\Leftrightarrow$ $a \le b$

上の定理では整数の値が付いたゲーム同士の直和は整数同士の和，比較も整数の比較で行えるということです．
上の定理と表3から， $B = 1 > 0$ なのでBは左勝ち， $WW = -2 < 0$ なのでWWは右勝ちのゲームとなります．

次に，他のゲームの値である2進有理数を定義します．

[定義：2進有理数]
整数 $j > 0$ ，奇数 $m$ に対して，
　 $\frac{m}{2^j} = \left\{ \frac{m - 1}{2^j} \mid \frac{m + 1}{2^j} \right\}$
とする．

先ほどの整数と同様に，2進有理数の値が付いたゲーム同士の直和は2進有理数同士の和，比較も2進有理数の比較で行えます．
有限のゲーム木に対応する数は整数と2進有理数のみですが，有限でないゲーム木にまで拡大すると，実数，順序数およびそのほかの数を含む超現実数(surreal number) が得られます．
今回のBWBゲームでは有限のゲーム木のみを扱うので，整数と2進有理数のことを数と呼ぶことにします．

6. BWBゲームの解法

6.1 [BWBゲームのゲームの値]

BWBゲームで現れるすべてのゲームの値は数になります．初めに，BWBゲームに数を割当てる方法を天下り的に説明します．

$n$ 個の箱からなる1つの山のゲームの値を求めます．この値は数 (整数または2進有理数) となります．

1山のゲームの値の割当て方
入力：　 $n$ 個の箱からなる1つの山 $G$ ．山の下から連続する同じ色の箱の数を $m$ ．
出力：　 $G$ の数 $val$

val = 0  // Gのゲームの値 (数)

if (G の一番下の箱の色が黒)
    val = m;
else // G の一番下の箱の色が白
    val = -m;
    
for (i = 1; i <= n - m; ++i) {
    if (下から m + i 番目の箱の色が黒)
        val += 1.0 / pow(2, i);   // 1 / 2^i を加える
    else if (下から m + i 番目の箱の色が白)
        val -= 1.0 / pow(2, i);    // - 1 / 2^i を加える
}

return val;

例：ゲームBBBWBBWの値)
ゲーム BBBWBBWの値は次のようになります． $n = 7, m = 3$ です．
　BBBWBBW = $3 + \left(-\frac{1}{2}\right) + \frac{1}{4} + \frac{1}{8} + \left(-\frac{1}{16}\right) = \frac{45}{16}$

例：ゲームWWBWWの値)
ゲーム WWBWWの値は次のようになります． $n = 5, m = 2$ です．
　WWBWW = $-2 + \frac{1}{2} + \left(-\frac{1}{4}\right) + \left(-\frac{1}{8}\right) = -\frac{15}{8}$

複数の山からなるゲームはそれぞれのゲームの直和になるのですが，ゲームの値が数ならばその加算，減算を行うことで簡単に計算が出来ます．

例：2つの山からなるBBBWBBW.WWBWWのゲームの値)
　BBBWBBW + WWBWW $= \frac{45}{16} + \left(-\frac{15}{8}\right) = -\frac{547}{360}$
このゲームの値は負になるので，表3から右勝ちのゲームとなります．

例：3つの山からなるB.WB.WBのゲームの値)
　B + WB + WB = $\left(1\right) + \left((-1) + \frac{1}{2}\right) + \left((-1) + \frac{1}{2}\right)$
　　　　　　　= $\left(1\right) + \left(-\frac{1}{2}\right) + \left(-\frac{1}{2}\right) = 0$
このゲームの値は0になるので後手勝ちのゲームとなります．

ここまでは天下り的にBWBゲームに対して値を割当ててきましたが，どのように考察すればよいのかについてここでは説明していきます．そのために，次の定理を利用します．

[定理：ゲームが数となるための条件]
ゲーム $G$ のすべての左選択肢 $G^L$ と右選択肢 $G^R$ が数であり，かつ $G^L < G^R$ が成り立つならば， $G$ は $\mathscr{g}^L < x < \mathscr{g}^R$ を満たす最も簡単な数 $x$ である．

ここで， $\mathscr{g}^L$ は左選択肢の最大値， $\mathscr{g}^R$ は右選択肢の最小値とする．

ここで，選択肢がすべて数ならば劣位な選択肢の除去から左選択肢と右選択肢の個数はそれぞれ1個以下になります．上の定理にある最も簡単な数とは次の通りです．

[定義：最も簡単な数]
数 $x^L < x^R$ に対して， $x^L < x < x^R$ を満たす最も簡単な数 $x$ とは，次のどちらかによって定まる数

$x^L < x < x^R$ を満たす整数 $n$ が存在するならば， $x$ はそのような $n$ の中で最も絶対値の小さい整数
1が成り立たない場合， $x$ は $x^L < \frac{i}{2^j} < x^R$ の中で $j$ が最小となる2進有理数

ゲームBBBWBBWの値を上の定理を用いて求めてみます．下の箱から1個づつ加えていきながら値を求めていきます．
Step 1. ゲームBBB
第5章の整数から BBB = $3$

Step 2. ゲームBBBW
　BBBW $= \{BB, B, \_ \mid BBB\} = \{2, 1, 0 \mid 3\} = \{2 \mid 3\}$
$2 < 3$ なので上の定理を用いて $2 < x < 3$ を満たす最も簡単な数 $x$ を求めます．
$x$ は最も簡単な数の定義の条件2から $\frac{5}{2}$ となります．
したがって，BBBW = $\frac{5}{2}$

Step 3. ゲームBBBWB
　BBBWB $= \{BBBW, BB, B, \_ \mid BBB\} = \left\{\frac{5}{2}, 2, 1, 0 \mid 3 \right\} = \left\{\frac{5}{2} \mid 3\right\}$
同様に， $\frac{5}{2} < x < 3$ を満たす最も簡単な数 $x$ は $\frac{11}{4}$ なので，
　BBBWB = $\frac{11}{4}$

Step 4. ゲームBBBWBB
　BBBWBB $= \{BBBWB, BBBW, BB, B, \_ \mid BBB\} = \left\{\frac{11}{4}, \frac{5}{2}, 2, 1, 0 \mid 3 \right\} = \left\{\frac{11}{4} \mid 3\right\}$
同様に， $\frac{11}{4} < x < 3$ を満たす最も簡単な数 $x$ は $\frac{23}{8}$ なので，
　BBBWBB = $\frac{23}{8}$

Step 5. ゲームBBBWBBW
　BBBWBBW $= \{BBBWB, BBBW, BB, B, \_ \mid BBBWBB, BBB\} = \left\{\frac{11}{4}, \frac{5}{2}, 2, 1, 0 \mid \frac{23}{8}, 3 \right\} = \left\{\frac{11}{4} \mid \frac{23}{8} \right\}$
同様に， $\frac{11}{4} < x < \frac{23}{8}$ を満たす最も簡単な数 $x$ は $\frac{23}{8}$ なので，
　BBBWBBW = $\frac{45}{16}$

$i - 1$ 番目のステップで得られるゲームを $G_{i-1} = \{x_{i-1}^L \mid x_{i-1}^R\}$ としてそのゲームの値を $x_{i - 1}$ とします．また，山の下から連続する同じ色の箱の数を $m$ とします．
上の考察から $i$ 番目のステップで得られるゲーム $G_{i}$ の値 $x_i$ を求めます．
・下から $m + i$ 番目の箱が黒色の場合
　 $G_{i} = \{x_{i-1}^L, x_{i-1} \mid x_{i-1}^R\} = \{x_{i-1} \mid x_{i-1}^R\}$
・下から $m + i$ 番目の箱が白色の場合
　 $G_{i} = \{x_{i-1}^L \mid x_{i-1}, x_{i-1}^R\} = \{x_{i-1}^L \mid x_{i-1}\}$
$m + i$ 番目の箱が黒色なら $x_{i-1} < x_{i} < x_{i-1}^R$ を満たす最も簡単な数，白色なら $x_{i-1}^L < x_{i} < x_{i-1}$ を満たす最も簡単な数となります．これは，それぞれ $x_{i-1}$ に $\frac{1}{2^i}$ か $-\frac{1}{2^i}$ を加えることに等しくなります．

6.2 [BWBゲームの解法]

数をゲームの値として持つゲームの帰結類は表3から $\mathscr{P}, \mathscr{L}, \mathscr{R}$ のいづれかになり， $\mathscr{N}$ 局面になることはありません．したがって，公平な初期局面とは $\mathscr{P}$ 局面に対応するので，いくつかの山を選びそのゲームの値の和が0となるものの中で箱の数の和が最大となるものを選ぶという問題となります．BWBゲームを定式化すると次の通りです．

BWBゲームの解法
$i \in \{1, \ldots, n\}$ 番目の山の箱の数 $l(i)$ ，ゲームの値 (整数または2進有理数) $s(i) \in \mathbb{Q}$

最大化： $\sum_{i \in X} l(i)$
　制約： $\sum_{i \in X} s(i) = 0$
　　　　 $X \subseteq \{1, \ldots, n\}$

$l(i)$ は山に含まれる箱の数を数えるだけなので簡単にできます．また， $s(i)$ は 6.1 のアルゴリズムを用いて計算できます．このとき， $s(i)$ の値は数 (整数または2進有理数) となるので有理数型か倍精度浮動小数点型で値を保持します．この前処理には高々 $40 \times n$ の計算時間しかかかりません．
$\sum_{i \in X} s(i) = 0$ は部分和問題で $n \le 40$ なので半分全列挙で $O(n 2^{n/2})$ の計算時間で求めることができます．蟻本のpp.147にナップサック問題を半分全列挙で解いているのでそれを参考にすると良いと思います．

例：B.W.WB.WB)
各々の山の $s(i)$ と $l(i)$ を求めます．

B：　 $s(1) = 1$ ，　 $l(1) = 1$
W ：　 $s(2) = -1$ ，　 $l(2) = 1$
WB：　 $s(3) = -\frac{1}{2}$ ，　 $l(3) = 2$
WB：　 $s(4) = -\frac{1}{2}$ ，　 $l(4) = 2$

$\mathscr{P}$ 局面となる組合せは $X_1 = \{1, 2\}, X_2 = \{1, 3, 4\}$ です．このとき， $X_1$ の箱の数の和は2， $X_2$ の箱の数の和は4 となるので最大となる選び方は $X_2$ で4です．

例：B.W.WB.WB.BWW.BWW)
各々の山の $s(i)$ と $l(i)$ を求めます．

B：　 $s(1) = 1$ ，　 $l(1) = 1$
W ：　 $s(2) = -1$ ，　 $l(2) = 1$
WB：　 $s(3) = -\frac{1}{2}$ ，　 $l(3) = 2$
WB：　 $s(4) = -\frac{1}{2}$ ，　 $l(4) = 2$
BWW：　 $s(5) = \frac{1}{4}$ ，　 $l(5) = 3$
BWW：　 $s(6) = \frac{1}{4}$ ，　 $l(6) = 3$

$\mathscr{P}$ 局面となる組合せで箱の数が最大となる選び方は $X = \{1, 2, 3, 5, 6\}$ で箱の数の和は 10です．

6.3 [BWBゲームについて]

natsugiriさんのブログにも書かれていますが，BWBゲームは枝分かれのないLR-ハッケンブッシュというゲームになります．また，今回説明したゲームの値の割当て方はヴァンルード(Thea van Roode) によるものです．このことは，参考資料「組合せゲーム理論入門」のpp.137-138に書かれています．
始めの方でBWBゲームを左と右が同じ選択肢を持つことができると変更したゲームはニムというゲームになり解析が簡単になると言いましたが，左と右の打つ手を次のように変更したゲームはどうなるでしょうか．

アリスの手番：1つの山から黒色の箱を1つ選び，その箱とその上または下にあるすべての箱を取り除く．
ボブの手番：1つの山から白色の箱を1つ選び，その箱とその上または下にあるすべての箱を取り除く．

このゲームはドミノ倒しというゲームになります．残念なことに，ドミノ倒しのすべてのゲームはBWBゲームのように値が数になるとは限りません．ただ，次のようにいろいろな名前の付いたゲームの値が現れ楽しいゲームとなっています (組合せゲーム理論入門 pp.134-136)．

BBBBBBBB $= 8$
BBBBWWWW $= \pm 3$
BW $= *$
BWWB = $= \uparrow$
BWBWBWBWB = $= \frac{1}{16}$
BWBWBWBW = $= *4$

最後はグランディ数です．

7. まとめ (感想)

読んでくださって有難うございました．さらっと書いてさらっと投稿しようと思ったのですが長ったらくなってしまいました．また大事な部分の考察が間に合わずに中途半端な記事になってしまったことを反省します．
追記・修正したのでとりあえずは完成となります．

明日の担当はhama_duさんの「(\(⁰⊖⁰)/)(\(⁰⊖⁰)/)(\(⁰⊖⁰)/)(\(⁰⊖⁰)/) |＿|＿|＿|」とkenkooooさんの「Mi_Sawa さんに刺されない✨最大フロー🎀💕」です．
hama_duさんの記事は一体何が書かれるのかタイトルから想像出来ないので楽しみです．kenkooooさんは刺されないか心配です．

8. ソースコード

#include <bits/stdc++.h>

using namespace std;

class BlackAndWhiteBoxes {
public:
    BlackAndWhiteBoxes(int n) : n(n), pile(n, make_pair(0.0, 0)) {}
    void Input();
    int MaximumBoxes();
private:
    int n; // 山の数
    vector<pair<double, int>> pile; // pile[i] := i番目の山のゲームの値，箱の数

    double GameValue(const string p);
};

double BlackAndWhiteBoxes::GameValue(const string p) {
    int idx = 1;
    while (idx < p.size() && p[0] == p[idx])
        ++idx;

    double v = (p[0] == 'B' ? idx : -idx);
    for (double two_pow = 2.0; idx < p.size(); two_pow *= 2.0, ++idx)
        v += (p[idx] == 'B' ? 1.0 / two_pow : -1.0 / two_pow);

    return v;
}

void BlackAndWhiteBoxes::Input() {
    string p;
    for (int i = 0; i < n; ++i) {
        cin >> p;
        pile[i] = make_pair(GameValue(p), p.size());
    }
}

int BlackAndWhiteBoxes::MaximumBoxes() {
    const int n1 = n / 2, INF = 40 * 100;
    vector<pair<double, int>> vl(1 << n1, make_pair(0.0, 0));
    for (int i = 0; i < 1 << n1; ++i) {
        for (int j = 0; j < n1; ++j)
            if (i >> j &1) {
                vl[i].first += pile[j].first;
                vl[i].second += pile[j].second;
            }
    }

    sort(vl.begin(), vl.end());

    int max_size = 0;
    for (int i = 0; i < 1 << (n - n1); ++i) {
        double sum_v = 0.0;
        int sum_len = 0;

        for (int j = 0;  j < n - n1; ++j)
            if (i >> j & 1) {
                sum_v += pile[n1 + j].first;
                sum_len += pile[n1 + j].second;
            }

        auto it = lower_bound(vl.begin(), vl.end(), make_pair(-sum_v, INF));
        if (it != vl.begin())
            --it;

        if (max_size < it->second + sum_len && it->first == -sum_v)
            max_size = it->second + sum_len;
    }

    return max_size;
}

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);

    int n;

    cin >> n;
    BlackAndWhiteBoxes bwb(n);
    bwb.Input();

    cout << bwb.MaximumBoxes() << endl;

    return 0;
}